
Earlier this year I wrote a
post about analytic geometry. In that blog post I introduced you to the
coordinate plane,
points,
vectors,
segments, and all sorts of useful operations in 2D. The
dot and
codot operators, and their relation to being able to say things like "to left of" and "to right of" were discussed. Also, the relationship between
polygon area and its
orientation. In this post, we'll go a bit further into the 2D analytic geometry domain, discuss why it is important, and show a few results. And I will actually explain how to use dot and codot.
In 1975, Tom Schaefer introduced me to these concepts while clicking his ball-point pen nervously.
Yet his guidance was like gold to me. I had just received the keys to the kingdom of analytic geometry.
I was familiar with the dot and cross products from my schooling in 3D analytic geometry I received from an ex-Lockheed employee named Mr. Pearson who taught at De Anza near where I lived. But I was still naive about 2D analytic geometry. At Calma, programming CAD software for chip-makers, I learned that the dot and the codot were very useful in 2D as well.

The 2D
dot product (explained in my
earlier post) can determine whether two vectors point in the same direction.
When they do, the dot product is positive. By the way, if you divide the dot product by the product of the lengths of the two vectors, you get the cosine of the angle between the vectors. The resulting quantity is exactly one when the vectors point in the exact same direction. And it is exactly zero when the two vectors are perpendicular.
This is quite the same as dotting two
normalized vectors (vectors that have been divided by their lengths so that their new length is exactly one).

If the dot product is negative, however, then the vectors point in opposite directions. In clearer terms, v2 is more than ninety degrees away (in absolute value) from v1's direction when the dot product is negative.
So we can use the sign of the dot product to determine in which half-plane the endpoint of v2 resides. We will make use of this fact later in this post.
The dot product is easy to evaluate: given two vectors you multiply the x's together to make one product, multiply the y's together to make a second product, and add the two products together to make the dot product.

The 2D
cross product (
codot) shows whether two vectors define a counterclockwise or a clockwise angle.
When the codot is positive, the vectors make a counterclockwise (mathematically positive) angle. And similarly to the dot product, if you divide the codot product by the product of the lengths of the two vectors, you get the sine of the angle between the vectors. The resulting quantity is exactly zero when the vectors point in the exact same direction.
This fact can be used to determine whether the endpoint of v2 is to the left or to the right of vector v1.

If the codot is negative, then v2 lies to the right of vector v1, making a clockwise angle. This means we can use the codot to determine which half-plane that the endpoint of v2 lies. Another useful thing!
Evaluating the codot is a bit more complicated, but still easy to describe. The first product is the x from the first vector multiplied by the y from the second vector. The second product is the y from the first vector multiplied by the x from the second vector. Then the codot is computed by subtracting the second product from the first product.
With these newfound capabilities, I was suddenly empowered!
For instance, I was able now to compute the distance of a point from a segment easily, using the scalar cross product (also known as the codot operator). Why would I need this?
For one, when I needed to implement
pick. To pick something is to click or tap and be able to determine the nearest thing. This is useful when you need to select something to delete it, to edit it, or to move it. And in those days I was working with segments and polygons.
 Point-Segment Distance
Point-Segment Distance
To compute the distance between a
point and a
segment, we must consider all the cases. With a segment from point
p1 to point
p2, there are three cases. Either the point
p is closest to point p1, it is closest to point p2, or it in in the middle and it is closest to the segment. We can see these three cases in this diagram.
Isolines of equal distance from the segment basically look like a sausage, since they are rounded at the ends.
But how do we determine which case a new point will be?

We start by evaluating three
vectors, v1, v2, and v3. We start with v1, the vector from the start of the segment (point p1) to the end of the segment (point p2).
Vectors v2 and v3 are the vectors from point p1 to our point p and point p2 to our point p respectively. These will be used to determine locations and distances, the relationship of point p with the segment.

We can immediately see which case we are by using a
dot product.
Dot v1 with v2 to determine which side of point p1 the new point p lies.
Similarly, dot v1 with v3 to decide which side of point p2 the new point p must lie.
If it is within neither area A nor B, then it is in area C by the exclusion principle (which Sherlock Holmes was so fond of).
But what if the point is in area B? Then we must perform some slightly more complex computation.

Here we see vectors v1 and v2, which can also be used to determine the point segment distance. By using the
codot (scalar cross product) we can determine the sine of angle theta (shown in red).
As you can see, the dot and codot products are now becoming useful!

But this little diagram can give you a clue how to accomplish the computation. And also how to compute the signed distance.
Note that the sign of the distance is positive if the point p is to the left of the line from point p1 to point p2. And it is negative if p is to the right.
Thus, the point-segment distance in the most usual sense is the
absolute value of D.
Note also that D is simply the length of v2 when p is in area A (closest to p1). If p is in the area C (closest to p2), then D is simply the length of v3 instead.
Geometry is Complicated
Yes, geometry is quite complicated! Any kind of interesting operation usually becomes a miasma of cases and complexity. Just imagine how complex it is to determine if a point is inside or outside a polygon?
Well, you won't have to imagine because it is our next problem. First, a word on polygon representation.
 Where, Oh Where Has Polly Gone?
Where, Oh Where Has Polly Gone?
So let's return to the polygon. A
polygon is a ring of points connected by segments. Internally to a computer we represent it as a list of points, which is usually our first mistake. Well, at least it's the first thing that can go wrong, that lends it complexity, etc.
You see, a list has a start and an end, but a ring does not. This means we need to do one of two things: (Method 1) make the list longer by one element and thus represent the start and the end points redundantly, or (Method 2) make a simplifying implicit assumption that the last point of the list is actually followed by the first in the list (though it is not recorded redundantly).

The first method has the dubious advantage of having all the segments represented as a contiguous pair of points, but the disadvantage that the count of items in the list is one larger than the count of points in the polygon. This means you will always have to be adding or subtracting one whenever you deal with the polygon's points, and this is the root of
so many errors!
The second method has the advantage that the number of points is correct, but the disadvantage that one of the segments is not contiguous (the last one). This means that, whenever you have to enumerate the segments (in particular, the last one) you will have to do something special to see both points.
I prefer the second method. Because using the first method has come back to bite me more times than I can count! In fact, whenever I try to count the times, I always seem to be off by one! Ouch.
AC/DC Polygons?
The orientation of a polygon, which connotes whether it is clockwise or counterclockwise, can be determined by taking the sign of its area computed using the trapezoidal rule.
Some operations do not require the orientation to be known, like the test for whether a point is inside or outside the polygon. But if we need to make a local test for a point being inside or outside a particular edge of a polygon, orientation must be known. For instance, on a counterclockwise polygon, a right edge of the polygon goes in the upwards direction and the left edge goes in the downwards direction.
Some conditions confuse orientation, like self-intersecting polygons.
When you examine an ordinary (non-self-intersecting) polygon, that is oriented counterclockwise, you will find the right edges go from south to north and the left edges go from north to south. On a self-intesecting polygon this might not be the case.
Rules exist for deciding whether a point is inside or outside any polygon, including self-intersecting polygons. This includes the even-odd rule and the non-zero winding number rule. We will show how to implement these in the next section.

Holes are another quality that complicates polygons. Clearly you can't just treat a hole exactly like any other outside boundary polygon. But there are rules that can simplify our approach to holes.
When a polygon has holes, the convention is to orient the holes in the opposite way from the outer border of the polygon. So, a counterclockwise polygon has clockwise holes by convention.
And then there is the issue of islands. You can have a counterclockwise island inside the hole. And so forth and so on. So holes can have holes, but they are really outlines.
I told you that geometry was complicated!
 Vexing Convexity and Caving Into Concavity
Vexing Convexity and Caving Into Concavity
Knowledge of orientation makes possible some of the more complex operations on a polygon, like fracturing into convex pieces.
But before we can do something as complicated as fracturing, we have to have an intuitive notion of what is locally concave and what is locally convex. Fortunately the codot comes to the rescue.
In this diagram you see the right edges of two counterclockwise polygons. The one on the left is locally convex at point p2. The one on the right is locally concave at point p2.
I form vector v1 by subtracting p2 from p1 and vector v2 by subtracting p3 from p2. We can just use the "to left of" and "to right of" measures to decide whether the polygon is convex or concave at point p2.
You see, v1 codot v2 will be positive if the polygon is convex at point p2 and negative if the polygon is concave at point p2. This is another reason that the dot and codot operators are so useful.
Inside and Outside
Now we can look at the problem of deciding whether point p is inside or outside of a polygon.
To solve this we really have to ask ourselves whether polygon orientation is important to this crucial test. It's not as easy as all that to answer this question.
To solve this problem we need only draw a ray east from point p. If we count the number of intersections of this ray with segments of the polygon, we can determine if point p is inside or outside. If the polygon isn't self-intersecting, then it is pretty easy to see that the number of intersections of this ray with the polygon segments will be an odd number only when point p is inside the polygon.
But how many cases are there to consider?
What happens when the ray is collinear with a horizontal segment?
If the ray is a clean intersection with the edge, it's easy to see it will count. But when the ray intersects at a vertex, then it is more complicated to decide if the intersection counts. But there is a simple trick that can help us decide how to count these unusual intersections.

Here a ray is shown intersecting a vertex in different ways. Some intersections count, like the leftmost one, which goes from the inside of the polygon to the outside. Other intersections do not count, which merely graze the polygon in some way.
The clever trick is to consider the top vertex and the bottom vertex of the edge. If the intersection occurs at the top vertex, then it counts. If it occurs at the bottom vertex, then it doesn't count. In the leftmost case, only one of the two segments would then intersect the ray, which is correct. In the middle case, both segments would intersect the ray, and since we are looking at the parity of the intersections, that would mean that they cancel each other out. In the right case, no intersection would count since both intersections are at the bottom vertex of the two segments.

When the polygon is self-intersecting, however, this method produces an answer that enforces the even-odd rule, since we are looking at the parity of the number of intersections.
And this is where polygon orientation comes in.
To implement the non-zero winding number rule, we must consider how the ray crosses a segment. If the segment crosses the ray in an upwards direction, then we add one to the winding number. If the segment crosses the ray in a downwards direction, then we subtract one from the winding number.
At the end, if the winding number is zero, then the point is outside the polygon. Otherwise if it is positive or negative (non-zero) then the point is considered to be inside the polygon. This is a good reason to orient a polygon's holes in the opposite direction as their outside boundaries.
The winding number rule works correctly with the top-counts bottom-doesn't rule, also, and so we have a solution!
Lastly, an inside-ouside tester might also want to return a value of "on edge" in some cases.
Sharp, Distance
A distance function can be used to shade a polygon and this has an application to the tiling patterns I have been working with recently. It also has a bearing on a problem in printing.
Printers often want to spread or choke a given shaded area. This is because ink isn't perfect and tends to spread a bit when it is printed on paper. So a shaded area is often choked first, which enables the natural spread that occurs in printing to produce the right-sized result.
This technique is also used in e-beam lithography, which is the first place I encountered the problem of insetting a polygon.
You can consider the inset of a polygon to be the set of points that occur at a fixed distance inside the boundaries of the polygon. So the outside boundary gets choked and holes get spread.

Things like insetting and outsetting are fairly well understood, but did you know that the way we construct gables for the roof of a house is actually completely related to the distance function and thus can help us compute any inset?
Here is a simple house's gabling as viewed from above. On a roof of a house, lines of equal elevation represent specific insets of the perimeter of the house.
So if I produce the gabling for an arbitrary polygon, I can use that information to produce any inset I want. And also any beveling I want.

You can compute the gabling of an arbitrary polygon. The boundaries between facets are actually the bisectors between successive edges of the polygon. But when the bisectors meet, then we need to bisect the edges that are farther apart.
Computing the gabling for an arbitrary polygon is complex indeed! It borders on graph theory.
But it is useful in both beveling and also for computing the grout of a tiled pattern! More on this in my next installment of the Patterns series.
 The Tile Pattern Designer is coming along. In it, you design a tile pattern in a parallelogram repeat block. This gives you quite a bit of leeway, with the ability to design triangular and hexagonal tiles, as shown in Patterns, Part 5. Using a grid to design tile patterns in this way is sufficient to plot out most of the tile patterns from the floor of the San Marco Basilica in Venice, as shown in Patterns, Part 6.
The Tile Pattern Designer is coming along. In it, you design a tile pattern in a parallelogram repeat block. This gives you quite a bit of leeway, with the ability to design triangular and hexagonal tiles, as shown in Patterns, Part 5. Using a grid to design tile patterns in this way is sufficient to plot out most of the tile patterns from the floor of the San Marco Basilica in Venice, as shown in Patterns, Part 6.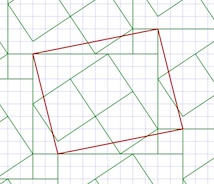 First I design a pattern by drawing lines between grid points. This one took only eight lines, using a slightly rotated rectangle as the basis. I am careful to leave a few unusual shapes for open areas. This is so I can show you how the beveling works later.
First I design a pattern by drawing lines between grid points. This one took only eight lines, using a slightly rotated rectangle as the basis. I am careful to leave a few unusual shapes for open areas. This is so I can show you how the beveling works later. Here I show the polygon areas.
Here I show the polygon areas. Next I bevel the edges of the polygons. This is actually complicated. It involves a gabling operation as we will see in a moment.
Next I bevel the edges of the polygons. This is actually complicated. It involves a gabling operation as we will see in a moment. The bevel width is controllable, allowing you to magically adjust the look of the tiles directly with a slider. For me, it's a bit disorienting to change the bevel width, because I am not used to seeing this occur in real time in the real world.
The bevel width is controllable, allowing you to magically adjust the look of the tiles directly with a slider. For me, it's a bit disorienting to change the bevel width, because I am not used to seeing this occur in real time in the real world. There is also a grout control. This means you can change the grout width in real time with a slider as well. This can make tiles that look a bit more real, since real tiles do have grout in between them.
There is also a grout control. This means you can change the grout width in real time with a slider as well. This can make tiles that look a bit more real, since real tiles do have grout in between them. The beveling is completely general. If you crank up the beveling width until it is large enough, the center parts of the tiles disappear. This is why I call this a gabling operation.
The beveling is completely general. If you crank up the beveling width until it is large enough, the center parts of the tiles disappear. This is why I call this a gabling operation. One more problem presented itself when I was building this tool: the matte edge problem. When rendering polygons that abut each other, you get a tiny matte edge. I have made the background black to make this more obvious.
One more problem presented itself when I was building this tool: the matte edge problem. When rendering polygons that abut each other, you get a tiny matte edge. I have made the background black to make this more obvious.










































